2024年广州一模数学单选压轴题分析解答与高考复习建议
一,题目呈现
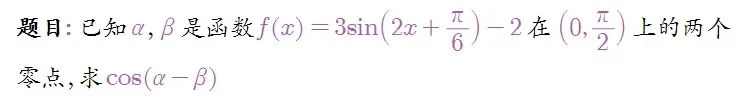
这道题是昨天考的广州一模的单选最后一题,题目质量很好,考察学生的分析问题解决问题能力,调用数学工具能力和数学运算能力。
二,题目分析和解答
1,考察“自然语言转化为数学语言”
α和β是两个零点这句话,学生能不能得到一个关于α和β的数学关系式?这需要学生熟悉三角函数的图像,实际上考察的是三角函数的对称性,两个零点关于三角函数的对称轴对称。因为两个零点在第一象限,所以这条对称轴也一定在第一象限。正弦函数函数对称轴就是经过正弦函数最高点或最低点且与x轴垂直的直线,容易看出当2x+π/6=π/2时,也即是x=π/6是对称轴,所以α和β关于x=π/6对称,进而α+β=π/3①。
2,考察化归思想
由于α和β是两个零点,根据零点的定义,化简可得
sin(2α+π/6)=2/3②,
sin(2β+π/6)=2/3③。
结合刚才得到的α+β=π/3,题目转化成了已知三个等式①②③,求cos(α-β)。至此,题目从定义,从图像 ,转到了三角运算。
3,考察数学运算数学素养
运算,不是硬算,更不是死算,而是在逻辑的指导之下,选择运算方向和运算策略,要算什么,什么是不需要算的,怎么算才最省时间,这些都是要考虑的。
解法1,消元思想指导下的运算
要我算cos(α-β),角α-β有两个变量,我可以用α+β=π/3①这个结论消掉一个变量,cos(α-β)=cos(2α-π/3)④,出现2α了,与②很像了,条件和要求的越来越接近了,很开心。cos(2α-π/3)和sin(2α+π/6)=2/3有什么联系呢?我相信这种题目大多数学生之前都做过不少。2α+π/6和2α-π/3相差π/2,cos和sin互化公式也是相差π/2,主要不要搞错符号就行,
cos(2α-π/3)=sin(2α+π/6)=2/3。
或者这样思考也行,2α-π/3逆时针旋转九十度,就是2α+π/6,单位圆上的点旋转了90°,(x,y)变成了(y,x),根据三角函数的定义,所以cos(2α-π/3)=sin(2α+π/6)=2/3。这就是考察三角函数的本质,点的坐标与旋转,根本没有用到什么公式。
解法2,综合法指导之下的运算
已知
α+β=π/3①,
sin(2α+π/6)=2/3②,
sin(2β+π/6)=2/3③。
求cos(α-β)。
由②和③,我用和差化积公式
sin(2α+π/6)+sin(2β+π/6)=4/3。
和化积公式,要把括号里面两个角化为他们的和的一半,差的一半。
括号里面两个角相加除以2,出现α+β,而α+β=π/3就是①,这是已知。
括号里面两个角相减除以2,出现α-β,而cos(α-β)就是所求。这样就实现了已知和求解的闭环 ,剩下来的就是计算而已。
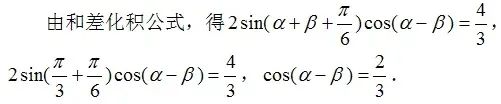
三,题目鉴赏题目难吗?难,也不难。难,难在分析问题。分析需要思维,所以这道题就是考察数学思维的一道好题。难在需要知道三角函数的定义,“定义,性质,图像,应用”是一个整体,它们统一于单位圆。大家只需搞定单位圆,三角函数题目怎么变都做得出。
不难,因为这些都是课本里面的知识,只要你老老实实把课本学懂,把知识的来龙去脉搞清楚,做出这道题不是难事 。曹凤山老师说解题要回到原点,王淼生老师说要重视概念。这道题的原点和概念的重点就是三角函数的定义以及由定义生成的性质。上课的时候,教师把知识的来龙去脉搞清楚,重视知识的生成性,那学生就学得透。
这道题符合高考命题方向,是一道质量非常高的题目,高考应该多考类似题目,才能起到引导教学和反刷题的指挥棒作用。
四,复习建议离高考只有不到三个月,高三学生老老实实回归教材,回归基本概念,回归基本方法。
高考容易题,中档题,难题的比例是3:5:2,普通学生把注意力放在这道题前面的3和5这80%题目上面,这些都是考察基础。这道题也是考察基础,是中档题。最难的30分,普通人放弃就好,放弃30分你还有120分,普通学生关键是基础题不丢分,而不是抢难题的分。










